| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- CI/CD
- CORS
- async/await
- RTK Query
- webpack
- SSR
- useAppDispatch
- autosize
- React
- recoil
- Promise
- TS
- 투포인터
- 리터럴 타입
- 공변성
- 태그된 유니온
- 타입 좁히기
- 인터섹션
- Jest
- ESlint
- 호이스팅
- map
- dfs
- 결정 알고리즘
- MSA
- 반공변성
- 인증/인가
- tailwind
- app router
- 무한 스크롤
- Today
- Total
짧은코딩
그래프(1) 본문
완전 그래프
각 정점에서 다른 모든 정점을 연결해 최대로 많은 간선 수를 가진 그래프
무방향 그래프 최대 간선 수: n(n-1)/2개
방향 그래프 최대 간선 수: n(n-1)개
그래프 구현
-인접 행렬
무방향 그래프

방향 그래프
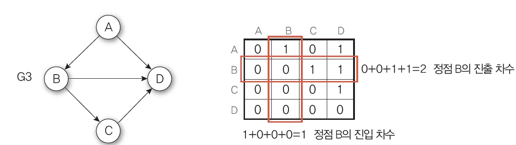
-인접 리스트
무방향 그래프

방향 그래프

그래프 순회
-깊이 우선 탐색, DFS
시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이를 탐색해 가는 법
가장 마지막에 만났던 갈림길 간선의 정점으로 가장 먼저 되돌아가서 다시 깊이 우선 탐색을 반복해야 하므로 후입선출 구조의 스택 사용

1. A를 시작으로 깊이 우선 탐색 시작
스택: Null
2. A에서 방문하지 않은 정점 B, C가 있어서 A를 스택에 push, 이 중에서 오름차순에 따라 B를 선택
스택: A
3. B에 방문하지 않은 정점 D, E가 있어서 B를 스택에 push, 이 중에서 오름차순에 따라 D를 선택
스택: A B
4. D에 방문하지 않은 정점 G가 있어서 D를 스택에 push, G를 탐색
스택: A B D
5. G에 방문하지 않은 정점 E, F가 있어서 G를 스택에 push, 오름차순에 따라 E를 선택
스택: A B D G
6. E에 방문하지 않은 정점 C가 있어서 E를 스택에 push, C를 탐색
스택: A B D G E
7. C에서 방문하지 않은 정점은 없어서 E를 삭제
스택: A B D G
8. G에서 방문하지 않은 정점 F가 있어서 F를 탐색
9. 스택에서 맨 위에 정점에서 방문하지 않은 정점이 없으면 스택이 없을 때 까지 계속 삭제
-너비 우선 탐색, BFS
시작 정점을 결정하여 방문하고 인접 정점 중에서 방문하지 않은 정점을 차례로 방문하면서 큐에 enQueue한다.
방문하지 않은 인접한 정점이 없으면 큐에서 deQueue하고 큐가 공백이 될 때까지 반복

1. A를 시작으로 너비 우선 탐색
큐: Null
2. A에서 방문하지 않은 모든 인접 정점 B, C를 방문하고 큐에 enQueue
큐: B C
3. 정점 A에 인접한 정점들을 처리했으므로 다음 정점을 찾기 위해 deQueue를 하여 B를 받는다.
B를 삭제하고 D, E를 삽입
큐: C D E
4. 정점 B를 처리하고 C를 삭제하고 C의 인접 정점을 처리한다. 하지만 C에는 방문하지 않은 인접 정점이 없다.
큐: D E
5. 정점 D를 삭제하고 인점 정점 G를 처리한다.
큐: E G
6. E에는 방문하지 않은 인접 정점이 없어서 E를 삭제하고 G에서 인접 노드를 찾는다.
큐: G
7. G에서 방문하지 않은 정점 F를 방문한다.
큐: F
8. F는 모드 인접 정점을 방문해서 큐에서 삭제
큐: Null
신장 트리

신장 트리: n개의 정점으로 이루어진 무방향 그래프에서 n개의 모든 정점과 n-1개의 간선으로 만들어진 트리
깊이 우선 신장 트리: 깊이 우선 탐색을 이용하여 생성된 신장 트리
너비 우선 신장 트리: 너비 우선 탐색을 이용하여 생성된 신장 트리
최소 비용 신장 트리
무방향 가중치 그래프에서 간선들의 가중치 합이 최소인 신장 트리
- 최소 비용 신장 트리를 만드는 알고리즘
1. 크루스칼의 알고리즘
2. 프림의 알고리즘
-크루스칼의 알고리즘Ⅰ
가중치가 높은 간선을 제거하면서 최소 비용 신장 트리를 만드는 방법
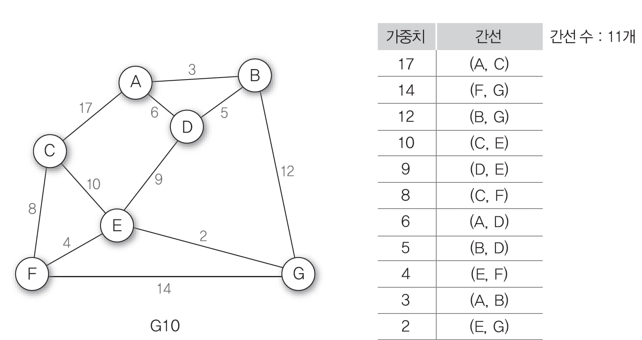
그래프 G10의 간선을 가중치에 따라 내림차순 정렬 -> 가중치가 높은 간선부터 제거한다.(간선이 n-1개가 남을 때까지 반복)

쭉 제거하다가 (D, E)를 제거해야 하는데 (D, E)를 제거하면 그래프가 분리되어서 다음으로 가중치가 높고 분리가 안되는 (A, D)를 제거
-크루스탈 알고리즘 Ⅱ
가중치가 낮은 간선을 삽입하면서 최소 비용 신장 트리를 만드는 방법

그래프 G10의 가중치에 따라 오름차순으로 정렬 -> 위에서 부터 간선의 수가 n-1이 될 때까지 삽입

(A, D)를 삽입했는데 사이클이 생성되어 삽입할 수 없고 다음 간선을 삽한다.
-프림 알고리즘
간선을 정렬하지 않고 하나의 정점에서 시작해 트리를 확장해 나가는 방법
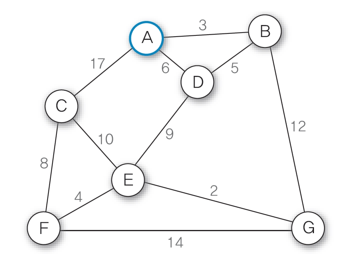
시작 정점을 선택 -> 인접 노드 중에서 가중치가 가장 낮은 간선을 연결하여 트리 확장 -> 이전에 선택한 정점과 새로 확장된 정점, 2개에서 연결된 모든 간선 중에서 가중치가 낮은 간선을 삽입(사이클이 이루어지면 안됨) -> n-1개가 삽입될 때까지 반복
(A, B) -> (B, D) -> (D, E) -> (E, G)

여기서 G의 인점 노드 가중치는 커서 그 전에 들렸었던 E의 인접 노드 중 가중치가 작은 F로 간다.
(A, B) -> (B, D) -> (D, E) -> (E, G) -> (E, F)
(A, B) -> (B, D) -> (D, E) -> (E, G) -> (E, F) -> (F, C)




